Lendo um artigo científico - parte 8 - é diferente, mas tem significado clínico?
- Paulo Henrique Orlato Rossetti

- 7 de jul. de 2025
- 3 min de leitura
Atualizado: 20 de jan.

Se você está chegando agora nessa seção do blog, não se preocupe. Há uma lista de posts comentando a leitura da estatística. Comece pelo número 1.
Agora, caso você seja mais experiente, continue daqui.
Existem duas perguntas frequentes ao refletirmos sobre o resultado de uma análise estatística em meta-análise:
primeiro, deu diferença, mas será que tem algum significado clínico?
segundo: se tem impacto clínico, qual é a sua intensidade?
Vamos ao exemplo de uma situação clínica comum em pesquisa: um biomaterial para ser colocado dentro de um alvéolo porque o dente será extraído e isso representa uma tentativa de atenuar o grau de remodelamento ósseo vertical e horizontal.
Você não sabe se isso é bom ou não é. Não leu ainda os estudos publicados.
Para preservar a saúde do seu paciente você vai até à biblioteca (eletrônica ou não), coleta informações, e monta um gráfico de bosque /floresta (forest plot) com alguns estudos tentando entender o que também está acontecendo do ponto de vista clínico.
Gráficos de floresta possuem dois elementos comuns: os intervalos de confiança 95% e os effect sizes.
Quando falamos em tecido ósseo, é bem provável que o nosso effect size seja a diferença entre os valores de perda e ganho ósseo provocados pela inserção do biomaterial.
Então, como de costume, montamos um gráfico onde o valor zero é o nosso indicador de referência no eixo X: assim, tudo o que estiver à esquerda do valor zero é considerado perda, e tudo o que estiver à direita do valor zero é considerado ganho, como no exemplo abaixo:

Intervalos de confiança = o valor da diferença estatística é significativo?
Agora, se você lembra bem, no gráfico de floresta, colocamos linhas horizontais que representam esses intervalos de confiança 95%.
Entretanto, no exemplo abaixo, vou colocar apenas os as linhas horizontais (intervalos de confiança 95%), observando se esses intervalos cruzam ou não cruzam o valor de referência zero (seta escura):
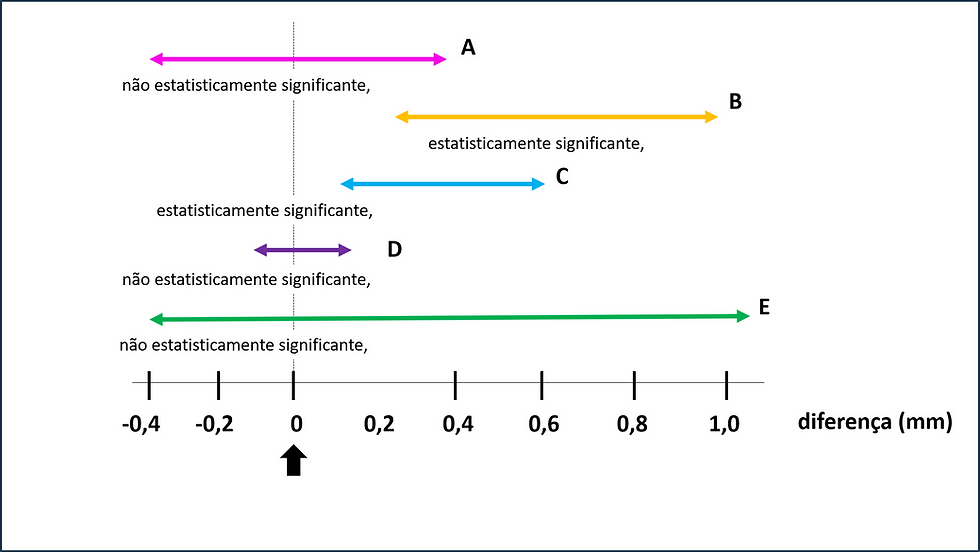
No gráfico acima, cada letra maiúscula representa um estudo e seu intervalo de confiança 95%: veja que os estudos A, D, E cruzam a linha do zero. Então, podemos considerá-los não estatisticamente significantes. Já os estudos B e C não cruzam essa linha do zero, e assim podem ser considerados estatisticamente significantes.
O intervalo de confiança, no gráfico de floresta, indica o aspecto da estatística (ser ou não a diferença entre ganho e perda óssea estatisticamente significativa).
Effect size: o valor do significado clínico seria real?
Vamos continuar: no gráfico abaixo, vamos posicionar os effect sizes (riscos verticais coloridos) para observamos outro aspecto: será que o effect size de cada estudo tem alguma importância clínica? Observe que o limite clínico minimamente importante em relação à remodelação óssea, definido no gráfico abaixo imaginário, tem valor 0,2 mm.

No gráfico acima, comparamos a posição de cada risco vertical colorido com o valor de referência 0,2mm: os riscos dos estudos A e D estão posicionados antes do valor referência 0,2mm e são considerados clinicamente não importantes. Já os riscos verticais dos estudos B, C, e E estão posicionados á direita do valor de referência (0,2mm) sendo considerados clinicamente importantes e em graus variados de importância.
O effect size, no gráfico de floresta, mostra se a diferença entre ganho e perda óssea é ou não clinicamente importante.
Unindo a estatística com a clínica
Agora, agrupando todos os dados (intervalos de confiança 95% e effect sizes) no mesmo gráfico de floresta, teremos o aspecto abaixo:

No gráfico final acima, conseguiremos finalmente perceber que, nem sempre o que é estatisticamente significante, também tem importância clínica.
Um dos grandes problemas, especialmente nos estudos clínicos, consiste em definir o que é clinicamente importante.
Bons estudos!!!




Comentários